PLAYER

IT GUIDES of USER

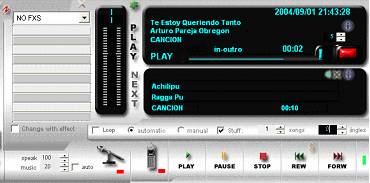
The Reproducer without none he/she doubts, it is the most important screen in WIT, the control center and emission.

OPERATION DE THE REPRODUCER: PREFERENCES

To big features we will say that WIT is based on a new emission system by areas, more concretely four areas, where the first one is the one that has more preference and the fourth the that less. With only to give to the PLAY, the one reproducer starts.

When pressing PLAY the reproducer he/she starts.

1

First he/she goes to the area of PUBLICITY and it stops to see if it should emit some announcement. If he/she doesn't find none he/she goes to the HOTZONE.

2

Second he/she goes to the HOTZONE if he/she finds some I file in this area it reproduces it. If he/she doesn't go to PROGRAMS

3

Third go to PROGRAMS, if he/she finds some I file it reproduces it. If there is not it happens I stuff (If it is activated).

4

Room if the option filler is selected it will load

a half file at random.

As the reproducer it works it is the most important part of WIT, some minutes of reading and 1 hour of practice is more than enough for to learn it, computer science's knowledge is not required for its use.

·               Panel digital of control

·               Accesses to menus.

·               Panel of files stocking

·               Hotzone

·               Publicity

·               Programs

·               Emission

. Vumeter compressor

. Menus

. Chat

. Tools control

. Tele-scroll

. Info

. Monitor cue

. Meteorological station

. Keys functions

. Color Skins

PANEL DIGITAL OF CONTROL

In the superior part of the screen. this screen is mainly indicative and informative.

We can right encontrar(superior) the file mediates that he/she is reproducing: title, author, remaining time and the one I file that is in wait.

Fx´s insole seleccionada(superior left), this insole consists of 10 special goods that you/they reproduce pulsing from the key F1 to the F10. To select an insole it is necessary to go to the panel of files stocking-Fx and to select FXS.

To change with effect: it is option is under the fxs, it means that when a song change takes place to song, so that this it changed it is more spectacular and creative during the beginning of the same one he/she will reproduce a fx automatically, in each I change one beginning with the first one, later the first one and this way consecutively.

Manual- automatic: (to the derecha)se refers to the operation of the reproducer, if it is in automatic the changes they are carried out so that when one finishes song reproduces automatically the other one. If the manual option is the selected one it means that after each song there is that to press PLAY so that he/she reproduces the one that is in he/she waits, that is to say after each song he/she stops. The default option is automatic.

Filler: Wit when it is in automatic shape it reproduces a song and when finishing it reproduces the one that is in wait, if there is not none in wait you for. If we have the activated option filler, he/she won't stop if not that one will choose at random and it will put it in wait to reproduce, so that he/she will never stop.

x Songs x Masks: Option related with the previous one I stuff, it means like the aleatory system of selection will work for the one I stuff, each how many songs are to put a certain number of masks, if we want that it puts three songs and later two masks and so forth, we will put: 3 songs 2 masks.

FIRST WE SHOULD To SELECT THE MASKS that will put on in the filler in in wità padded playeràschedulingàcaretas

Microphone: When pressing the microphone the channel he/she opens up of the mixer and it lowers the volume according to the securities that we have en  the following options:

Speak: volume of the microphone

Music: volume of the music when the one microphone is open

Car: if we select this option when we begin to speak the level of music bajará       automatically. It is a car fader. It requires that the sound compressor be active.

The line of the microphone is configured in wità playeràconfiguracionesà configuration you generate it vozàid micro

Telephone: It is good to pass the sound of the calls in direct. We will configure the modem, saying him which it is the com that uses in wità playeràconfiguracionesà configuration generates it telephone, also right here we will be able to configure the level to that the music should go down I go a long way let us have the active telephone.

HE/SHE NOTICES: The filler doesn't influence on the publicity scheduled programs to emit, that is to say if we have an announcement for the 15.30 hrs and the program it works in padded way when it arrives at that hour the announcement it will be emitted and then it will continue with the filler. The same thing if it is time to emit a it programs, it will emit it and when finishing it will continue with the filler.

It activates textvoice: This active option the way of presentation with artificial voices. If when we have created the program hemos  written text in the area help of each song is it will be transformed into voice. To remember that if when creating the program we have given him the option of active textvoice, automatically to the one to load it the option will be activated and when finishing this program it will be disabled.

Play: It begins the reproduction, or the it continues if you had pressed pause. If there is not anything selected but the way I stuff it is selected, he/she will begin at random with a song.

It pauses: He/she stops the reproduction.

Stop: He/she stops the reproduction.

Setback: It begins the song or file ab initio again.

Advance: It happens to the following song or file. If we are reproducing a song and we have another in wait, will stop the first one and the one will begin that is in wait.

Filter: it filters the listings of songs and masks

INFORMATION GROUPS SONGS

Press the drawings in leaf form and it will have all the information of the song, group or artist

PANEL OF FILES STOCKING

The function of this panel is clear and concise: it is where you they select the files so that they are loaded in the HOTZONE of the reproducer, files that will be emitted soon.

Inside this panel of files stocking we find eight remote

Bellboys comunes to all:

It DARTS of the right it loads the file selected in the hotzone.

LANTERN is good to look for files for the one name, as well as we go writing the files that coincide appear.

RE if we write the number of the song or another half file and we press the it darts of to the side, it is immediately loaded in the hotzone.

He/she ADDS it determines if when loading a file in the hotzone will be added to the end of the list or se                                     it will insert between two files.

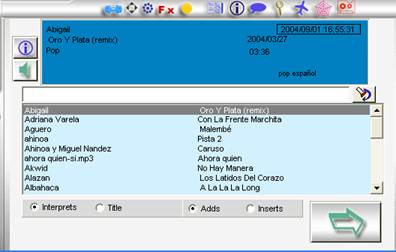
Songs

Here we select the song that we want to load in the HOTZONE.

We can look for for letters.

Preescucharlas (CUE).

To order them for title or interpreter.

We also have a screen of information with the styles, it dates of high, album, duration.

He/she tells us the DATE and HOUR of the last time that it was emitted the song, appears in the right superior frame.

Masks

Here we select the masks that we want to load in the HOTZONE.

We can look for for letters.

Preescucharlas (CUE).

We also have a screen of information with those styles, it dates of high, duration.

Publicity

Here we select the advertising announcements that we want to load in the HOTZONE.

We can look for for letters.

Preescucharlas (CUE).

We also have a screen of dated information of high, duration.

Fx

Here we select the Fx that we want to load in the HOTZONE.

We can look for for letters.

Preescucharlas (CUE).

We also have a screen of dated information of high, duration

From Here the insoles of Fx´s are also loaded , of the player

That they are 10 goods that you/they are shot with the keys F1.F10

Several

Here we select the several ones that we want to load in the HOTZONE.

We can look for for letters.

Preescucharlas (CUE).

We also have a screen of dated information of high, duration.

Programs

In this section we select a program of the list and it is loaded in the "area it programs", when being loaded if there were files in the hotzone, they are eliminated.

Help

In this section it is where the annotations, script or text appear of the program.

Let us remember that we can write what we will say us, what you/they will say the voices artificial or annotations, when creating a program. To each file multimedia will correspond him a space help and this way as he/she goes reproducing the program, the Help will go changing.

The text of the HELP is the one that appears in the Tele - Scroll

Voice

This section is good us to write any word or sentences so that in an instantaneous way when pressing the textvoice button Play, be read by the artificial voices.

We have the option to select the artificial voice that we want.

PRESENT INTRO/OUTRO

Here it is where seleccionamos  the voice of the presentations of the songs that we have recorded by our own speakers. They are recorded in wità playeràpresentaciones vozàcanciones files stocking

Styles

Here it is where we select the filters so that those searches and the files stocking are quicker.

We can apply filters to songs, masks and several.

And we can filter for styles, gender, dates of high, year.

Connections

Here we can load an internet connection . sat. aux in a manual way and also to begin and to finish a remote pause, so that the local radio stations they can emit their publicity.

Play 1: it begins a pause so that the other radio stations emit their publicity

Stop 1: for the remote pause

Play 2: it loads an internet connection / sat / aux

Stop 2: for the current connection.

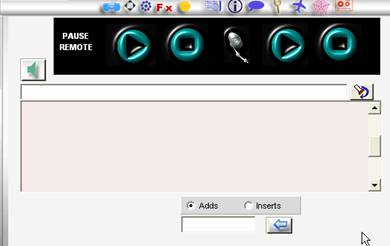
Record  WEEK  timer

Here we have the information of the recordings that we have programmed for the day.

Week: We can program recordings weekly indicating the hour of beginning and of end.

Rec    :   opens record manager

Acm format: it is the format of compression that will be used for the recordings.

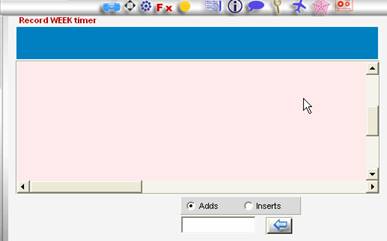
Rapid Player

It is an instantaneous and RECHARGEABLE reproducer of files from the same player.

We can also make rapids insoles, to already have the rapids prepared.

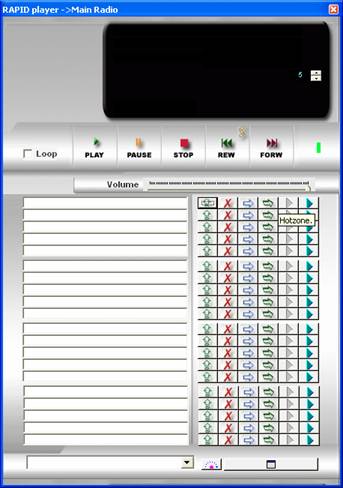
Witàplayeràrapidsàmantenimiento

blue play : it reproduces

gray play: he/she leaves the rapid in wait and he/she will reproduce when it finishes the one that is reproducing.

H: it loads the rapid in the hotzone of the player

N: it loads the rapid in the next of the player

Rubber to erase: it erases the rapid

It darts blue: it loads the file he/she mediates that we have pointed out in the half files of the player.

I square white: it loads us a rapid hole

It rotates: it changes title to interpreter and vice versa.

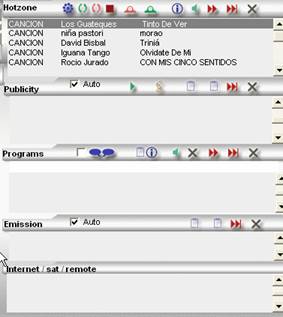
HOTZONE

In the hotzone it is where they are loaded the files that we load so that they are reproduced proximamente .

PUBLICITY

In this area we can see the publicity it programs, day hour and advertiser, when arriving automatically to that hour and day the programs it emits it.

We can choose the form of how it will interrupt the emission to emit the publicity:

Exact: Short the reproduction and it reproduces immediately the announcement.

Close: He/she waits to that finishes the file that is reproducing and next it emits the publicity. It substitutes the file that is in "NEXT." ( RECOMMENDED )

Standard: It loads the announcement when it is free the one "NEXT", doesn't cut neither it substitutes the file that is in "NEXT"

These options are in wità configuracionesà configuration you generate it publicity

IT PROGRAMS

When loading a program in the panel of files stocking, he/she will appear in this area.

EMISSION

In this area we find the list of the programs that you they will emit automatically orderly for date and hour. To program a program so that it is emitted to one hour and day certain we should :

1. To create a programa   wità playerà programasà maintenance

2. To go to wità schedulingà programmer of emissions to indicate the day and hour of emission.

VUMETER COMPRESSOR

Wit incorporates a vumeter real of the exit of the card of audio that us it indicates the sum of all volumes of the card of audio, what allows us a total control of the volume.

Car Nomalizer Compress : This option activates us the compressor that will correct us on time real those differences of volume among the music that we are reproducing, if it has been too high engraving will lower it, and if it is too low it will go up it so that let us emit a constant level of sound. The parameters of the compressor those we find in :

wità configuracionesà configuration generates it compressor

We should keep in mind that the compressor consumes resources of the computer, therefore you should configure it according to the capacity of our teams.

MENUS

Televisor              active  :  the tele - scroll for the reading of texts and scripts

Libreta           :  notebook for annotations

Email              :  opens the screen of email shippings

Navigator : he/she opens us a navigator web

News player : he/she opens the reproducer of news

News seeker  :  the searcher of news opens up so that we can load them in the hotzone

Rapids            :  opens us the one rapids reproducer

CHAT / net

It is good us to communicate among any Pc of the net, if we don't have the Player open, he/she communicates through the Monitor Studio.

It affects the Pc´s in net of the same radio.

TOOLS CONTROL

Car:     emits the publicity automatically, interrupts the emission according to the parameter defined in :

wità configuracionesà configuration generates it publicity

he/she can ser : it fences, exact, standard

Play: loads and it emits the siguiente  advertising block, in a manual way.

To : inform on the pending publicity of emitting, computer per hours and for companies.

>> : it loads the announcement in the hotzone

Rubber to erase: it eliminates the selected announcement of the list

To activate textvoice: Active the voices of MsAgent that you/they will read the text written in the info help of the file.

To: Report on the program

Leaf:       opens up the screen of the info of the file

Monitor cue:       for to make the preescucha of the file

Rubber to erase 1: it eliminates all the files of the one it programs

àà: loads the file in the hotzone and it eliminates of the hotzone all the previous ones

>> : it loads the file in the hotzone

Rubber to erase 2: it eliminates selected file of the it lists

Monitor cue:       for to make the preescucha of the file

àà: loads the file in the hotzone and it eliminates of the hotzone all the previous ones

>> : it loads the file in the hotzone

Rubber to erase: it eliminates selected file of the list

Leaf:       opens up the screen of the info of the file

Publicity Blocks: to insert masks

We can tell to Wit that when will put an advertising block it puts:

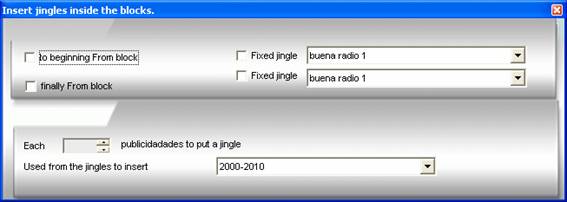
Before beginning one mask

When finishing another mask

A mask each a certain number of announcements

To select that type of masks debit side to use.

REPLAY

The function replay, returns to to reproduce the file ab initio.

Here we can select like we want him to be carried out this returned at the beginning.

Replay mix: carrying out a mixture

Replay cut: an immediate cut

Fx: that it shoots a fx, when beginning the file again, we should select the effect that we want.

TELE - SCROLL

The Tele-scroll is good to slip texts so that the speaker he/she can read them.

We can:

To regulate the speed

That he/she goes up or down

That he/she stops in each page

That he/she repeats loop

Advance and setback quick

Default the play and the stop is controlled from the bar espaciadora.

The Tele.scroll it slips the texts of the Help of the songs or of a it programs, we can also load manually texts and independent.

When we work in net and with locution study, this function is activated from the Study monitor, and everything is synchronized automatically by the player, in the terminals. For that that our speakers in the locution study will have the whole information of times of the songs, and they will be activated the tele-scroll automatically.

INFO

When selecting any button info of the player it takes us to this screen that gives us information on the song and the group.

This information is believed and he/she stays in witàplayeràinfo

MONITOR CUE

The monitor cue allows us to make preescuchas of the files stocking in a card of audio different to the one that is used to reproduce the sound of the air.

The card of sound of the monitor is configured in witàconfiguracionesàconfiguración generalàaudio devices

When we make preescuchas of files that are in the hotzone and in the next , we will also be able to vary the beginning moment or final, to adapt it to our necessities.

The monitor admits all type of files stocking, even video, divx, vcd, mpg, etc. All the compatible formats with WMP9.

STATION METEREOLOGICA

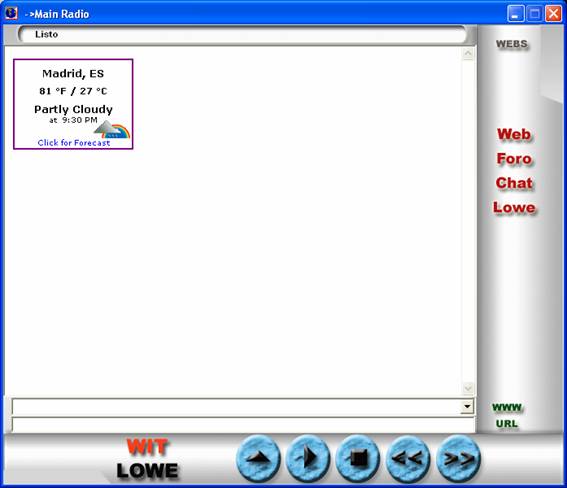
It is the finder that indicates the temperature and he/she gives access to the meteorological information of your city.

To activate it you should go to:

witàconfiguracionesàconfiguración generalàmeteorología

It is upgraded every 30 minutes

It requires internet connection active.

If we pulse on this screen we will consent c another screen with all the particulars on the forecast of the time.

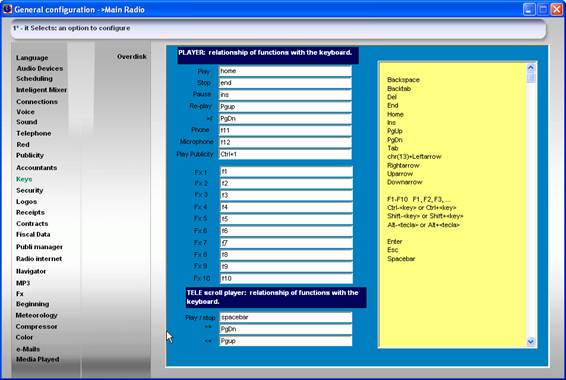
KEYS FUNCTIONS

They are those keys that control the functions of the player from the keyboard.

We can to relate the keys with the functions in :

witàconfiguracionesàconfiguración generalàkeys

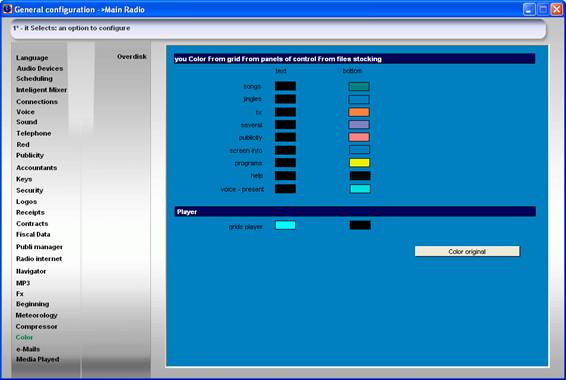
COLOR PLAYER AND SKINS

They are those color of the player these they can modify in:

witàconfiguracionesàconfiguración generalàcolores

The skins is the funds of the player, every time that we press skins, he/she goes changing.